Leetcode算法在生产中的实际应用
现在硅谷大厂小厂招聘都要面试leetcode上面的算法题。时不时就有人跳出来质疑这里面的意义,说在工作中又用不上这些东西,有的人甚至说自己做了好多年程序员了都没有用上过。
首先,面试面算法题的意义,我先强调一下。第一,证明应聘者的学习能力,或者说智商。第二,证明你的代码能力,动手能力。第三,过滤口若悬河却没有实际工作能力的应聘者。
这篇文章的重点不是这个,这篇文章的重点是在要证明实际生产中这类算法真的很重要。我们最近在某保险集团产险部门做了一个项目。其中有一个业务逻辑,就是要校验一个人的最高保额有没有超过限额。如下图,某被保人,已经买了保单1和保单3,现在要买保单2。现在要计算投保人在保单2的保险时间范围内的总保额。
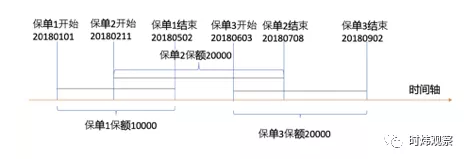
客户以前的算法是这样的,将被保人的所有与新保单有时间交叉的历史保单取出来,然后把这些保单的保额加在一起。那么这个例子中的总保额就是10000+20000+20000=50000。客户AI中心的领导亲自跟我们头脑风暴的时候就质疑了这个算法。他认为被保人的最高保额应该按照这个人在新保单的时间区间内的每个时间点的总保额的最高点计算。也就是说在这个例子中,最高保额是20180603到20180708之间的40000。他的这个定义非常的合理。那么问题来了,一个人的历史保单可能上百条,甚至上千条记录。而一个新保单中,按照我们的业务需求设计,会有2000个被保人。于是我们需要设计一个足够高效的算法来计算这个最高保额。你有没有感觉到一点leetcode的气息。OK, 大佬提出问题,众小弟展开思考。很快我们就设计出了一个时间复杂度为O(nlog n)的算法:
首先将保单的起止时间分开存成(time, tiemType, amount)的结构,其中timeType标记是开始时间还是结束时间,amount是保单的保额。然后将这些时间节点排序,从前面往后遍历,记录一个当前保额和最大保额,遇到开始点的时候当前保额就加上这个点对应保单的保额,遇上结束点就减去对应保额,如果当前保额超过最大保额,就更新最大高额。排序时间只要O(nlog n), 后面遍历只要O(n), 总时间复杂度不就是O(nlog n)。
好了,问题解决了。其实,最初我们想到的是一个更优的O(n)的算法。O(n)的算法某种角度说就超出了leetcode的范围。我们只要将历史保单起止点分开按时间顺序存在Cassandra数据库中,那么我们取出数据来就直接是排好顺序的,省去排序一步,时间复杂度就只有O(n)了。由于在数据库中分开存保单起止时间太tricky了,不好维护,就没有在生产中实际应用。客户还顺便拿这个有趣的应用申请了一个小专利。没想到吧,leetcode题目在生产中应用得好都能申请专利。
后来,我同事说其实leetcode上有一道类似的题目。这个题目就是一个公司需要安排一个会议,每个人提供一些available时间段,请你求出available人数最多的时间段。
你可能会说,你不就遇到了一次而已嘛。那好,我再给大家举一个例子。我们在量化交易中,有时候需要计算一个滑动的时间窗口的n个价格中的第k大的价格。最傻瓜的算法是排序然后取第k个数,复杂度为O(nlog n)。懂点算法的人可以很容易的得出一个O(n)的算法。可是还不够快。因为我们需要回测足够长的时间的市场行情,希望几分钟内就得出结果,要不然都没法调参数,O(n)的算法可能需要几个小时甚至几十个小时。最后我在这里应用了大名鼎鼎的红黑树,复杂度只要O(logn)。这是我2013在九坤实习的时候的事情,前几天,和这家前公司的朋友聊天的时候,他跟我说我写的这个算法他们还一直在用。这个算法,让我们回测许多策略成为了可能。
好了,其实吧,如果你只是刷题刷得熟练,应付面试可能没问题,要达到在生产中灵活应用这些算法的水平可能又是另一回事了。
往期回顾